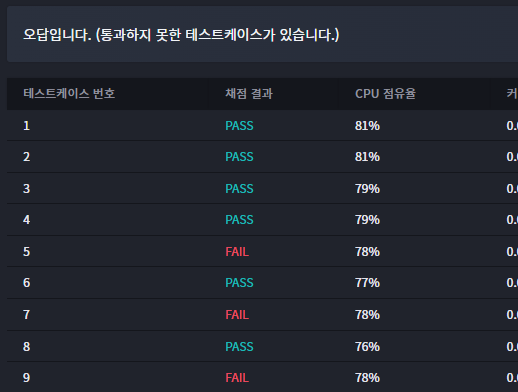
📌문제2G-버블정렬 구현하기
데이터의 수를 N이라고 하자. 아래의 과정을 N번 반복한다.
- 배열의 0번 칸의 숫자가 1번 칸의 숫자 보다 크다면 두 값의 위치를 교환한다
- 배열의 1번 칸의 숫자가 2번 칸의 숫자 보다 크다면 두 값의 위치를 교환한다
- ...
- 배열의 N-2번 칸의 숫자가 N-1번 칸의 숫자 보다 크다면 두 값의 위치를 교환한다.
입력 형식
첫 줄에는 데이터의 수를 나타내는 자연수 N이 주어진다. N은 1이상 1,000이하의 자연수이다.
두 번째 줄에는 공백으로 구분된 N개의 정수가 주어진다. 모든 정수는 32비트 정수형 데이터이다.
출력 형식
한 줄에 N개의 오름차순으로 정렬 된 숫자들을 공백으로 구분하여 출력한다.
예시
- 입력
5
35124
- 출력
1 2 3 4 5
생각 풀이
입력이 아래와 같다면 하나씩 열어본다. 모든 배열을 찾아 나보다 크다면 바꿔!
3, 5, 1, 2, 4
3이 기준이야.
3 : 3
5가 나왔네 ,, 3보다 크네 바꾸자.
3 : 5
5 : 1
5 : 2
5 : 4
3 : 5
5 : 5
5 : 1
5 : 2
5 : 4
1 : 3
3 : 5
5 : 5
5 : 2
5 : 4
2 : 1
2 : 3
3 : 5
5 : 5
5 : 4
4 : 1
4 : 2
4 : 3
4 : 5
5 : 5
1 2 3 4 5
코드 풀이
public static void bubbleSort(int[] data, int n) {
for(int i = 0 ; i < n ; i++){
for(int j = 0; j < n; j++) {
if(data[i] < data[j]) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
}
}
📌문제2H-픽셀 수 세기
컴퓨터는 이미지 정보를 2차원 배열 형태로 저장한다. 하지만 현실의 사물들의 모양을 그대로 저장하는 것은 불가능하다. 정밀한 이미지를 저장할수록 더 많은 공간과 연산량을 필요로 하기 때문이다. 영상을 구성하는 하나의 픽셀은 정사각형 형태로 존재하며 이 픽셀들이 모여 2차원 배열의 모양을 구성하게 된다.

반지름이 5픽셀인 원을 비트맵 형태로 저장하면 위와 같다. 그림에서 알 수 있는 것 처럼 실제로 원에 포함되는 픽셀들은 아래와 같은 특징을 가진다.
- 네 점이 모두 원 안에 존재하거나
- 원과 겹치는 영역이 존재하면서 두개 이상의 변이 원의 외곽선과 교차한다.
그렇다면 반지름이 임의의 R픽셀인 원이 포함하는 픽셀의 수를 계산하는 프로그램을 작성해보자.
입력 형식
이 문제는 여러 개의 테스트케이스로 구성되어있다. 첫 줄에는 테스트케이스의 수를 나타내는 1이상 10이하의 자연수 T가 주어진다.
각 테스트 케이스는 한 줄로 구성되며 계산하고자 하는 원의 반지름의 픽셀 수 R이 주어진다. R은 1이상 10만 이하의 자연수이다.
출력 형식
각 테스트케이스를 두 줄에 걸쳐서 출력한다.
- 테스트케이스의 첫 줄에는 테스트 케이스의 번호를 #1, #2, #3, ... 형태로 출력한다
- 테스트케이스의 두 번째 줄에는 반지름이 R픽셀인 원이 포함하는 픽셀의 수를 출력한다.
예시
- 입력
2
1
5
- 출력
#1
4
#2
88
생각 풀이
- 네 점이 모두 원 안에 존재하는가 ?
- 원과 겹치는 영역이 존재하면서 두개 이상의 변이 원의 외곽선과 교차한다. => 제외
2차원 평면 상에서 격자의 수는 무한하게 많다.
하지만 정답이 될 수 있는 격자의 범위는 유한하다.
원을 4등분했을 때 1등분에 생기는 각 끝 모소리점을 R 이라고 한다면 나는 R+1 까지만 고려하면 된다.
내가 그림을 잘 못그린다. ㅋㅋㅋㅋㅋㅋㅋㅋ
아무튼 옆에 그림처럼 나누고 그 점을 R 이라하기
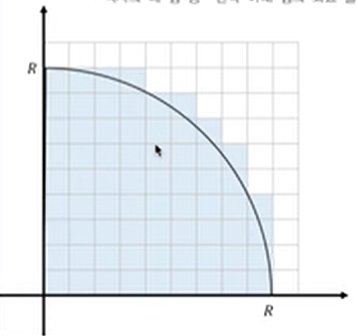
R 제곱개의 격자들 중 원에 포함되는 픽셀의 수를 세자.
- 각 격자를 구분할 수 있는 기준을 정해야 한다.
- 격자의 네 점중 왼쪽 아래 점의 좌표를 이용하자.
네 점 모두 원 안에 있거나, 두 개 이상의 변과 교체한다. => 영역교체
- 왼쪽 아래 점이 원 안에 있다.
public boolean inInside (long x, long y, long R) {
long sqd = x * x + y * y;
return sqd < R * R;
}
힛 사실 못풀겠다. 이해하는걸로 퉁 ~ !
📌문제2I-정주행
시간이 흘러 지구는 2100년이 되었고, 웹툰 마음의 소리는 10만회 이상을 연재하며 세계 기록을 매 번 갱신하고 있다.
대부분의 사람들에게 마음의 소리는 삶의 일부가 되었으며, 어린 학생들이 마음의 소리를 회차 순서에 맞게 쭉 정주행을 하는 모습을 쉽게 찾아 볼 수 있다.
하지만 조금 특이한 성격을 가진 승철이는 여태까지 마음의 소리를 순서에 구애받지 않고 읽어왔다.
그러던 어느날 승철이는 여태까지 자신이 본 에피소드의 번호들을 정렬하면 연속적인 수열로 표현될 수 있는지 궁금해졌다.
승철이는 마음의 소리를 다음과 같은 규칙을 지키며 읽었음이 보장된다.
- 승철이는 총 N화의 에피소드를 보았다.
- 승철이는 기억력이 좋기 때문에 똑같은 에피소드를 두번 보지는 않았다.
승철이가 여태까지 읽은 에피소드들의 번호가 차례로 주어질 때, 승철이가 본 에피소드들의 번호를 정렬하면 연속된 수열로 표현될 수 있는지 판별하는 프로그램을 작성하시오.
- 연속적인 수열이란 항상 i번째 숫자의 값이 (i+1)번째 숫자보다 1이 작은 정수로 이루어진 수열을 의미한다.
입력 형식
첫 줄에는 여태까지 승철이가 본 에피소드의 수 N이 주어진다. N은 1이상 10만 이하의 자연수이다.
두 번째 줄에는 승철이가 본 에피소드의 번호들이 공백으로 구분되어 주어진다. 에피소드의 번호는 모두 서로 다르며 1이상 100만 이하의 자연수이다.
출력 형식
승철이가 본 에피소드의 번호들이 연속적인 수열로 표현될 수 있다면 YES를 출력하고, 그렇지 않다면 NO를 출력한다.
예시
- 입력
5
1 2 5 3 4
- 출력
YES
생각 풀이
배열을 순회 한다.
그리고 모든 배열에 자신보다 +1 이거나 -1 인 수가 있는지 확인하고 없다면 false 를 반환한다.
내 답이 시간 초과가 나와서 쌤 답을 봤는데, 당연히 시간초과이겠거니 싶다.
코드 풀이
시간초과 ,,, ;;;
/**
* 배열의 N개의 원소가 연속적인 정수 수열로 표현될 수 있는지 판단하는 함수
* @param data
* @param n
* @return
*/
public static boolean isConsecutive(int[] data, int n) {
for( int i = 0; i < data.length; i++) {
for( int j = 0; j < data.length; j++ ) {
if(data[i] < data[j]) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
}
int startValue = data[0];
for( int i = 0; i < n; i++) {
if(data[i] != startValue++) {
return false;
}
}
return true;
}
쌤 답
/**
* 배열의 N개의 원소가 연속적인 정수 수열로 표현될 수 있는지 판단하는 함수
* @param data
* @param n
* @return
*/
public static boolean isConsecutive(int[] data, int n) {
// 최소
int l;
// 최대
int g;
int m;
l = g = data[0];
// 최대 , 최소 값 추출
for( int i = 0; i < n; i ++) {
if( l > data[i]) {
l = data[i];
}
if( g < data[i]) {
g = data[i];
}
}
m = ( g - l + 1 );
return m == n ? true : false;
}
모범 답안 생각 풀이
사용자가 6 개의 배열을 중복 수 없이 입력하였다고 생각해보자.
즉 , 6개의 숫자 => [ 5, 8, 7, 6, 9, 10 ]
그럼 여기서 최소값과 최대값을 구한다.
여기서 최소값은 5, 최대값은 10
최대 최소 값의 차이가 배열의 길이와 같아야 한다.
그리고 이건 공식이라고 한다.
최대값 - 최소값 + 1 공식을 기억하자 !
( 최대값 : 10 - 최소값 : 5 ) + 1 = 6 ====> [ 5, 6, 7, 8, 9, 10 ] == size : 6
( 최대값 : 5 - 최소값 : 3 ) + 1 = 3 ====> [ 3, 4, 5 ] == size : 3
( 최대값 : 8 - 최소값 : 1 ) + 1 = 8 ====> [ 1, 2, 3, 4, 5, 6, 7, 8 ] == size : 8
와 ,,, 진짜 유레카다 ㅠㅠㅠㅠㅠ 어떻게 이렇게 똑똑하냐 ㅠㅠㅠㅠ
📌문제2J-승부조작
같은 반인 현무와 재윤이는 이번 주 청소 당번이다. 현무와 재윤이는 서로 내기를 하여 청소일을 한 명에게 몰아주기로 하였다. 간단한 게임을 통해 지는 사람이 두 명분의 청소를 하기로하고 재윤이는 아래와 같은 게임을 현무에게 제안하였다.
- 재윤이는 총 N개의 종이컵의 안 쪽에 임의의 자연수를 적어둔다.
- 모든 종이컵은 숫자가 보이지 않도록 뒤집은 채로 일렬로 나열한다.
- 종이컵의 위치는 게임 도중에 변경될 수 없다.
- 현무는 임의의 인접한 K개의 연속된 종이컵을 선택하여 숫자를 확인하고 그 숫자들의 합을 구한다.
- 해당 숫자들의 합이 짝수이면 재윤이가 청소를 하고, 홀수이면 현무가 청소를 한다.
게임을 시작하기 전 현무는 재윤이가 숫자들을 자신이 이길 수 밖에 없도록 조작한 것이 아닌지 의심을 하게되었다. 하지만 재윤이가 워낙에 많은 종이컵을 준비해두었기에 일일이 확인을 해보기는 힘들었다. 현무는 당신에게 재윤이가 적은 숫자들로 게임을 진행할 경우 자신이 이길 수 있는 경우가 존재하는지 확인해달라는 부탁을 하였다. 현무를 위해 프로그램을 만들어주자.
입력 형식
첫 줄에는 종이컵의 수 N과 현무가 선택할 종이컵의 수 K가 공백으로 구분되어 주어진다.
N과 K는 1이상 10만 이하의 자연수이다.
두 번째 줄에는 총 N개의 종이컵에 적힌 숫자들이 실제 놓여진 순서대로 주어진다.
종이컵에 적힌 숫자들은 모두 0이상 100만 이하의 정수이다.
출력 형식
첫 줄에 현무가 이겨서 재윤이가 청소를 하게 될 수 있는 경우의 수가 존재한다면 YES를 출력하고, 그렇지 않다면 NO를 출력한다.
예시
- 입력
3 2
- 출력
NO
생각 풀이
코드 풀이
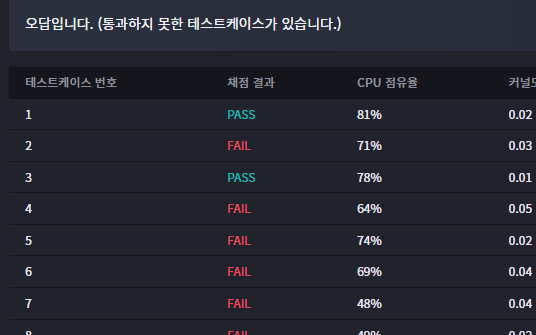
/**
* 게임의 규칙에 따라 현무가 승리할 수 있는 경우의 수가 존재하는지 검사하는 함수
*
* @param data
* @param n
* @param k
* @return true 현무가 승리할 수 있는 경우의 수가 하나 이상 존재한다면
* @return false else
*/
public static boolean isWinnable(int[] data, int n, int k) {
for( int i = 0; i < n-1; i ++ ){
if( ( data[i] + data[i+1] ) % 2 != 0) {
return false;
}
}
return true;
}
코드 풀이
/**
* 게임의 규칙에 따라 현무가 승리할 수 있는 경우의 수가 존재하는지 검사하는 함수
*
* @param data
* @param n
* @param k
* @return true 현무가 승리할 수 있는 경우의 수가 하나 이상 존재한다면
* @return false else
*/
public static boolean isWinnable(int[] data, int n, int k) {
for( int i = 0; i < n-1; i ++ ){
if( ( data[i] + data[i+1] ) % 2 == 0) {
return true;
}
}
return false;
}
코드 풀이
public static boolean isWinnable(int[] data, int n, int k) {
int sum = 0;
for( int i = 0; i < k; i ++ ) {
sum += data[i];
}
if( sum % 2 == 0 ) {
return true;
}
for( int i = 0; i + k - 1< n; i ++ ){
sum = sum - (data[i-1] + data[i+k-1]);
if( sum % 2 == 0 ) {
return true;
}
}
return false;
}'TEAM STUDY > 알고리즘 코딩 테스트 스터디' 카테고리의 다른 글
| 4회차 - 알고리즘 기록 : 페인트 (0) | 2022.06.13 |
|---|---|
| 4회차 - 알고리즘 기록 : 전화번호 (0) | 2022.06.13 |
| 2회차 - 알고리즘 기록 (0) | 2022.06.03 |
| 1회차 - 알고리즘 기록 (0) | 2022.05.21 |
| [charter1] 선형 알고리즘 기초 (0) | 2022.05.06 |